English readers : you can read this to get a taste of what this post is about.
C’est un jeu que j’ai découvert en farfouillant dans les notes de cours de Jean-Edouard Colliard. Il fait un peu penser au Risk, et se trouve être d’un jeu tellement débile que l’on ne voit pas ce qu’y peut faire la théorie des jeux. Il me fait un peu penser au jeu dont parle Richard Dawkins dans l’édition augmentée du Gène Egoïste.J’ai traduit la page de l’université de Leeds qui y est consacrée. En voici une version francaise html.Le jeu du colonel Blotto
Le jeu du du colonel Blotto, dans une de ses version, a pour règles les suivantes :Le colonel Blotto et son adversaire ont chacun 100 divisions, et vont devoir s’affronter sur 10 morceaux de territoire (régions). Ils doivent donc (Indépendamment) diviser leurs forces en 10 garnisons et envoyer chacune dans une région. Dix combats se déroulent, et celui pour qui la taille du régiment est la plus importante remporte le territoire (il peut y avoir égalité). Le vainqueur de la bataille est celle qui a remporté le plus de territoires.Exemple :Blotto divise ses forces de la manière suivante :
10, 10, 10, 10, 10, 10, 10, 10, 10, 10Son adversaire, rusé comme un renard, anticipe cela et partage ainsi ses forces :
11, 11, 11, 11, 11, 11, 11, 11, 11, 1.En conséquence, Blotto perd la bataille 9-1.Maintenant, il n’est pas difficile de démontrer que, étant donné n’importe quelle distribution des troupes , il en existe une autre qui peut la battre. Mais certaines distributions distributions sont clairement pire que les autres, par exemple 25 25 25 25 0 0 0 0 0 0 est tout à fait susceptibles de perdre 6-4 contre la plupart des formations opposées. La stratégie optimale est une sorte de stratégie mixte, mais trop difficile à analyser, autant que je sache (bien que l’on puisse des dans versions restreintes du jeu, par exemple 6 divisions et 3 régions, mener une analyse assez facilement.)Les règles de la compétition du colonel Blotto ayant eu lieu en Janvier 1990 étaient celles-ci : Les participants doivent me faire parvenir par e-mail une séquence de 10 nombres entiers positifs dont le total s’élève au plus à 100 Les séquences dont la somme vaut de plus de 100 au total seront disqualifiées. Après la date de clôture (à minuit le 31 janvier), je ferai se mesurer en un tournoi toutes les séquences les unes contre elles tournoi, comme ci-dessus, donnant 2 points pour une bataille gagnée, 1 point pour un un nul et 0 point pour une défaite, de sorte à ce que la marge réelle de la victoire (9-1, 6-4, ou quoi que ce soit d’autre) n’ait aucune incidence sur le score final. Le gagnant sera le participant ayant le score le plus élevé à la fin.Pas plus d’une séquence par personne ne sera acceptée.Pour le rendre le jeu plus intéressant, un petit prix de 5 livres sera décerné au gagnant (ou partagé entre les gagnants). La décision de l’arbitre est définitive.Notez également que l’ordre des positions est important, par exemple,
100 0 0 0 0 0 0 0 0 0 est différent de 0 100 0 0 0 0 0 0 0 0. Plusieurs personnes ont souligné la similitude entre ce jeu et d’autres tout aussi amusants. Jonathan Mestel a rappelé l’existence d’un Problems Drive (ndt:?) qui met en compétition plusieurs équipes, à qui l’on à donné 100 buts à marquer contre tous les autres des équipes dans un tournoi de football simulé. Peter Killworth celle d’un jeu de cartes à deux mis au point par Hubert Phillips: deux mains identiques , de 30 cartes chacune, sont obtenues en utilisant deux paquets. Les joueurs trient les cartes en six mains de Poker, et celles-ci sont jouées deux à deux, l’un après l’autre.Colin Wright a mené un jeu appelé
«Psychological Ju-jitsu», qui se déroule à peu près comme suit : on enlève les
cœurs d’un paquet de cartes, on donne les pics au joueur A, les trèfles au joueur B; cela qui laisse les carreaux à disposition, qui sont retournées une après l’autre . Chacun des deux joueurs mise ensuite simultanément en offrant un de ses cartes (noires) Une égalité fait que la carte est conservée et offerte avec la suivante (ou perdu en même temps, s’il s’agit du dernier coup). Il y a diverses manières de déterminer le gagnant: soit en comptant le nombre de carreaux gagnés, soit en comptant les têtes (1,2,3, …, 10, V = 11, D = 12, R = 13). Revenons-en au sujet. Voici le tableau final de la compétition du Colonel Blotto. Les joueurs sont identifiés par leurs identifiants informatiques
Numéro Joueur Disposition des forces........ V E D pts qui 26 17 3 17 3 17 3 17 3 17 3 64 33 9 161 PNT12 80 19 1 1 19 19 1 1 19 19 1 56 44 6 156 AG120 27 19 2 16 18 3 19 0 3 17 3 61 33 12 155 CDW10 39 1 19 1 1 19 19 19 1 19 1 54 46 6 154 BCK1 24 7 18 18 2 9 3 18 5 2 18 61 30 15 152 GRB10 82 2 10 1 18 19 3 20 2 8 17 61 26 19 148 JML11 3 17 0 17 0 17 0 16 0 17 16 64 19 23 147 JDG14 7 17 0 17 0 16 0 16 17 16 1 64 17 25 145 JPMG1 22 16 17 5 2 4 19 1 18 15 3 57 31 18 145 GKS1 38 16 0 17 16 0 0 17 17 0 17 64 17 25 145 RMR12 43 0 0 0 0 17 17 17 17 16 16 61 23 22 145 RDHW 4 17 15 0 0 17 17 17 0 0 17 59 26 21 144 CET1 66 1 17 1 1 21 19 17 1 1 21 50 41 15 141 MTB3 53 2 4 8 16 16 20 15 0 15 4 54 32 20 140 HTL10 35 6 6 16 6 16 16 6 16 6 6 55 29 22 139 JS138 17 5 10 18 16 1 5 18 16 10 1 56 26 24 138 SEW10 63 1 1 15 1 18 18 10 2 17 17 52 32 22 136 SV14 11 4 16 0 0 16 16 16 0 16 16 58 19 29 135 CRB11 42 18 0 18 18 0 10 18 0 18 0 46 43 17 135 MAW13 2 17 2 12 17 2 17 2 12 17 2 49 36 21 134 REB5 94 1 1 17 14 1 2 13 18 14 19 57 20 29 134 FM11 14 16 1 15 16 1 16 17 1 16 1 54 25 27 133 JBOM1 52 3 16 0 16 16 16 0 16 16 1 54 25 27 133 DRV10 58 1 16 1 16 16 16 1 16 16 1 51 31 24 133 SJ106 25 1 2 1 1 21 19 17 15 13 10 51 30 25 132 SKB13 54 1 1 1 1 16 16 16 16 16 16 53 26 27 132 EJH12 32 0 18 0 18 0 17 0 16 16 15 52 26 28 130 VAAP1 64 16 1 16 2 8 18 4 1 18 16 46 38 22 130 PER10 95 1 16 1 16 1 1 16 16 16 16 50 29 27 129 AGW14 100 5 12 20 3 8 6 13 21 4 8 45 39 22 129 AJG14 92 16 16 1 16 16 16 1 16 1 1 50 28 28 128 IR11 87 1 16 16 16 1 1 16 16 1 16 48 31 27 127 IF10 1 4 2 21 11 18 11 17 11 3 2 49 28 29 126 RJW15 75 1 16 16 1 1 16 1 16 16 16 47 32 27 126 KW102 81 1 16 16 1 16 16 1 16 16 1 46 34 26 126 RJS22 85 1 1 14 16 18 18 16 14 1 1 49 28 29 126 MJO11 91 1 16 16 16 1 1 16 16 16 1 47 32 27 126 BEQ10 44 1 16 16 16 1 16 1 16 16 1 45 34 27 124 MFSY1 59 16 1 16 1 16 16 1 16 1 16 49 25 32 123 TJC1 72 16 1 16 1 16 16 1 16 1 16 49 25 32 123 RDMG1 102 1 15 17 12 3 1 12 21 15 3 44 35 27 123 IG17 83 1 1 16 16 16 16 16 16 1 1 48 26 32 122 DJS6 71 3 14 2 16 14 15 16 2 15 3 49 23 34 121 DR105 10 18 1 1 16 15 1 15 16 1 16 50 20 36 120 RR108 73 2 2 3 8 14 13 15 17 14 12 39 41 26 119 APG12 13 6 16 6 6 16 6 6 16 6 16 35 47 24 117 DT108 90 1 1 15 18 15 15 18 15 1 1 48 21 37 117 RJB17 86 16 19 16 16 16 17 0 0 0 0 46 24 36 116 HHL10 5 0 2 4 6 8 12 14 16 18 20 41 33 32 115 CRJ10 15 18 0 20 0 24 0 20 0 18 0 24 67 15 115 XXM10 41 0 0 0 16 16 16 16 16 16 4 43 28 35 114 DTS12 89 15 8 17 16 3 1 3 15 13 9 42 27 37 111 MO101 107 2 20 6 8 16 4 12 14 18 0 36 39 31 111 JPM19 47 10 12 8 14 6 16 4 18 2 10 33 44 29 110 AJP15 93 17 17 17 16 15 14 4 0 0 0 50 10 46 110 AHS10 51 0 16 16 0 16 20 0 16 16 0 44 21 41 109 SMWI1 98 14 3 12 16 5 9 13 17 6 5 33 42 31 108 APS14 56 0 0 17 6 19 17 12 1 12 16 40 27 39 107 APAK 105 4 1 13 18 6 15 11 14 1 17 36 35 35 107 TJL13 28 0 0 21 2 24 22 1 23 3 4 40 26 40 106 RJD4 34 1 3 7 15 24 24 15 7 3 1 35 32 39 102 WYN10 9 2 10 8 18 12 12 18 8 10 2 30 40 36 100 LR106 16 1 19 3 17 5 15 7 13 9 11 30 39 37 99 ARP11 8 13 1 22 7 7 13 1 22 7 7 32 34 40 98 AG109 31 0 17 13 17 0 17 10 13 0 13 32 30 44 94 JDS11 57 6 7 8 10 11 20 11 13 4 10 27 39 40 93 DJC17 21 14 1 14 14 0 14 14 1 14 14 39 14 53 92 FJMT1 97 14 6 14 6 14 6 14 6 14 6 26 40 40 92 AK110 49 12 5 18 16 6 11 10 11 5 6 29 33 44 91 DRTR1 99 5 8 14 9 9 12 12 11 17 3 25 41 40 91 RJFH1 74 2 14 14 12 2 2 14 14 12 14 33 23 50 89 RJH21 76 15 2 15 3 14 10 13 2 12 14 31 27 48 89 RFD10 77 3 13 13 3 13 13 13 3 13 13 32 24 50 88 AJC21 40 15 0 15 15 0 15 0 10 15 15 32 23 51 87 PJB10 78 3 12 13 13 4 13 13 4 13 12 30 27 49 87 GJC11 79 0 17 15 13 10 0 13 15 17 0 33 21 52 87 MAE14 19 2 10 4 12 6 14 8 16 10 18 26 34 46 86 JMC17 106 17 1 12 14 18 12 6 9 5 6 27 32 47 86 RJS23 20 6 7 5 0 6 15 29 5 16 11 23 38 45 84 CR24 55 18 16 13 9 11 14 6 8 2 3 27 29 50 83 DAC11 12 4 13 13 13 13 1 13 13 13 4 31 20 55 82 PAS14 23 14 14 1 14 14 0 14 14 1 14 31 20 55 82 MRAO 29 0 17 18 0 11 12 11 14 4 13 28 26 52 82 JRXR1 88 1 1 14 14 14 14 13 14 14 1 33 15 58 81 SBR11 104 0 14 14 14 16 14 14 13 0 1 31 17 58 79 DSTM1 36 14 16 14 16 14 16 10 0 0 0 29 20 57 78 PRT10 18 15 15 15 15 15 15 10 0 0 0 32 13 61 77 TN101 69 4 11 12 18 20 10 8 12 5 0 18 40 48 76 GJCT1 30 17 16 15 14 13 12 11 1 1 0 28 19 59 75 SW118 65 16 15 13 1 14 16 12 0 12 1 33 8 65 74 WB103 45 15 3 32 1 16 2 8 4 4 15 19 33 54 71 BTCK1 84 12 14 4 4 12 14 10 14 12 4 25 21 60 71 JPAC1 60 0 15 12 11 12 0 14 12 11 13 25 14 67 64 SRW14 61 11 11 0 11 11 12 11 10 12 11 24 16 66 64 DKP10 67 12 10 13 2 4 13 12 9 12 13 21 22 63 64 IDR10 33 6 11 11 11 11 12 11 10 11 6 22 19 65 63 PGN10 70 8 8 12 8 12 8 12 8 12 12 18 26 62 62 DG106 6 8 5 10 12 8 10 11 16 8 12 19 23 64 61 NMM1 96 5 15 10 5 15 10 5 15 10 10 13 35 58 61 NKB11 68 13 12 13 13 0 12 12 13 12 0 24 10 72 58 MJB12 103 16 4 10 6 8 10 13 13 11 9 14 29 63 57 JMLW1 46 12 12 12 1 12 14 12 12 1 12 18 19 69 55 GS104 101 11 11 11 11 11 11 1 11 11 11 18 19 69 55 PD106 62 0 11 11 12 11 11 11 11 11 11 16 22 68 54 MM106 37 15 6 7 13 9 5 8 12 11 14 14 24 68 52 GDR11 48 10 10 10 10 10 10 10 11 11 8 16 20 70 52 MW121 50 7 3 14 11 2 5 9 6 1 42 2 27 77 31 DCC10
Le gagnant était donc Paul Taylor (PNT12).
Diverses stratégies ont été employées, et voici une sélection de certains des justifications formulées.Notons d’abord que le jeu est fortement non-transitif. Dans la version simplifiée à 3 régions et 6 divisions, 222 perd contre 330, qui lui perd contre 411, qui lui perd contre 222 à nouveau. Le but du jeu est donc de battre un maximum le plus possible d’autres participants, même si leurs propres stratégies peuvent varier considérablement. Cela rappelé à Ted Sohn une stratégie (illégale), appelée «titiller l’ordre des tables» dans des tournois d’échecs, où une équipe met un des ses joueur les plus faible sur le haut du tableau, dans l’espoir de faire un carnage dans la partie basse du tableau; au lieu de, comme on est censé faire, ordonner par niveau décroissant.Certains (Comme Nick Maclaren, NMM1 dans la notation du dessus) est allé droit chercher une distribution multinomiale, en utilisant un générateur de nombres aléatoires. David Robinson, DRTR1, un physicien, a misé sur une stratégie plus sophistiquée, en utilisant une statistique poissonienne . Apparemment, on peut montrer que cette distribution (au moins, dans la limite d’un nombre élevé de divisions par région) ) est celle qui maximise l’entropie (c’est une sorte de mesure du caractère aléatoire de la distribution) sous contrainte du nombre total de division. Il m’a dirigé vers un article de SF Gull (un autre physicien de Cambridge), intitulé: “Les singes, les kangourous et N.”Ceux qui sont sont orientés vers une stratégie plus déterministe ont tendance avoir de meilleurs résultats. Ils ont constaté que (comme le note Ian Farquharson, IF10, ) qu’il y a en fait deux problèmes distincts : le choix des nombres, qui doit pouvoir se prêter à une analyse rationnelle, et le choix de l’ordre, ce qui semble être purement psychologique dans un concours de ce genre, et qui doit donc être déterminé au hasard. Il semblait y avoir diverses théories suggérant qu’une stratégie des “6 grands” (la plupart des divisions concentrée sur six régions) aurait tendance à avoir de bonnes chances de gagner, parce que l’on serait susceptible de gagner 6 régions contre de nombreux adversaires. Cependant, un une stratégie des “5 grands” s’avère être meilleure encore, et chacun des 4 meilleurs participants ont fait ainsi. ceci.Alex Perry, ARP11, et quelques autres, ont sacrément fait chauffer leurs ordinateurs pour tenter de résoudre le jeu de manière “exacte” dans le cas d’un nombre moins important de guerre. Par exemple, il a conclu que, d’une certaine façon, la meilleure stratégie pour le jeu des 4 régions et 24 divisions (4/24) se trouve être 8 8 8 0, dans un certain ordre; pour le 4/28 il a trouvé 10 6 6 6; pour le 4/32 il a trouvé 11 7 7 7 et pour le 4/36 il semblerait que ce soit 12 12 12 0. Cela ne semble pas donner de piste valable pour le 10/100.Alex Selby, APS14, a procédé en essayant de résoudre les versions continues du jeu, par exemple : trois nombres non-entier dont la somme vaut 1 de chaque côté. L’avantage des versions continues, c’est qu’il y a toujours l’espoir que l’analyse mathématique puisse être utilisé. Cependant, même cette version semble être difficile, et la version à 10 régions est au-delà de des capacités de l’analyse.John Levine, JML11, a écrit un programme Lisp pour générer des séquences aléatoires les a fait jouer les unes contre les autres. Il a utilisé environ 5000 séquences et établi les scores; il a ensuite essayé de simuler le concours lui-même en jouant 30 séquences au hasard, 13 étant de bonnes séquences et 7 des perturbateurs (des séquences destinées à battre les bonnes des séquences ,comme par exemple 17 17 17 17 17 3 3 3 3 3 serait vaincu par 8 18 18 18 18 4 4 4 4 4). A sa grande stupéfaction, une des séquences aléatoires a gagné sa simulation de tournoi, avec une marge relativement importante; il a donc décidé de la jouer. Lors du vrai tournoi, elle s’en est plutôt bien sortie.Graham Brightwell, GRB10, a constaté que sa stratégie s’était très bien comportée contre les autres stratégies du top 12 (il en a battu 9 et fait 2 nuls), même si elle était moins efficace à battre les stratégies les plus faibles.Au final, tout le monde s’est bien amusé, si ce n’est le servie informatique, qui en a souffert. Ce jeu est fascinant, même si l’on ne le joue qu’ deux. Avec plus d’un centaine de participants, on a eu suffisamment de variété pour tester toutes les stratégies proposées.Cependant, on n’a pas dit le mot de la fin : John Levine a à nouveau fait tourner ses ordinateurs pour trouver une stratégie encore meilleure, en ce sens que si elle avait été en compétition avec toutes les séquences effectivement proposées, elle aurait gagné assez facilement. Cette séquence qu’il a obtenu était 2 3 0 3 17 17 18 17 17 6, et il aurait gagné avec un énorme 23 points d’avance. Il a obtenu ce résultat (selon ses propres mots) grâce à un processus itératif d’échange-et-incrément: prenez une séquence, regardez le score qu’elle obtient, ensuite soit échangez deux nombres plus (permutation), ou ajoutez 1 à l’un et retirez 1 à l’autre. Si le score augmente ou ne change pas, cette séquence devient la nouvelle meilleure. Bien sûr, tout cela s’appuie sur la connaissance préalable des autres séquences.Parfois, le recul est une chose merveilleuse.* *
*
Comme il s’agit d’un problème à plus de deux corps, le problème est chaotique (la moindre variation des conditions initiales a des conséquences importantes sur le résultat- effet papillon); les simulations sont faites en changeant très légèrement les conditions initiales et en faisant passer des milliards d’année. Si je me souviens bien, dans environ un scénario sur dix la Terre se cognait un jour où l’autre contre Mars ou Mercure. Gloups!
A propos de conditions initiales, voici une simulation de billard faite par l’excellent Paul Nylander qui donne le nombre boules empochées à la casse selon l’angle d’attaque et la force initiale. Fun!
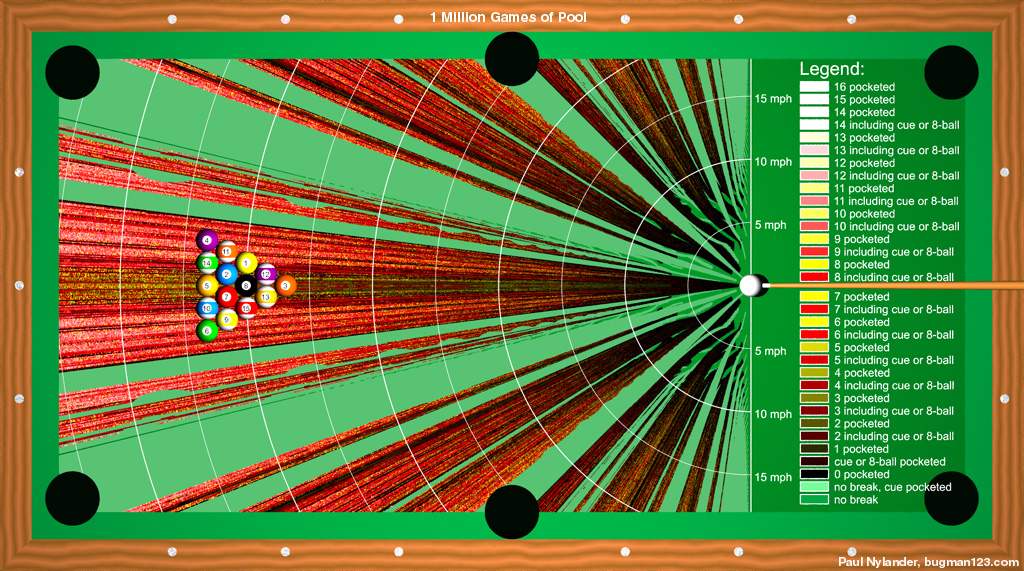
Illustration de la théorie du chaos sur un billard.